A Simple Market
This post is largely influenced by this article on medium. The author creates a simple simulation of a housing market in Python using the agent-based modeling framework Mesa. I chose to stick to basic Python packages for plots and numerical computations. Similarly to Patrick Labadie, the market is composed of $n$ agents making decisions on whether to buy or rent a house and there are $m$ houses available on the market.
The Agent class is initialized with a set of $5$ variables: a unique identifier for the agent, the market with which the agent interacts, a given level of income and wealth, both greater than $0$, and a budget defined between $0.2$ and $0.6$ which determines the maximal share of their income that the agent is willing to allocate to housing.
class Agent():
def __init__(self, id, market, income, wealth, budget):
self.id = id
self.market = market
self.income = income
self.wealth = wealth
self.budget = budget
self.status = "unhoused"
self.houses = []
self.rentPrice = -1
self.lease = None
The agents start as homeless and either accumulate houses or rent a house owned by another agent. Their status can take one of the following four values: unhoused, renter, owner, and investorTheir status depends on the number of houses they own. Investors own more than one house, owners own one house, and renters rent a house owned by an investor. Those without any housing solution remain unhoused.. The variable lease of any renter contains the house for which they must make rent payments at each step of the simulation.
The agents can engage in four actions, they can either buy or rent a house on the market and depending on their status, they can request or make rent payments. In order to buy a house, agents first check whether the house is available for purchase and whether its price is within their means. To simplify the decision making, agents buy houses based on their current wealth level without credit.
def buy(self):
for house in self.market.houses:
if house.status == "empty" and house.price <= self.wealth:
house.status = "rent" if len(self.houses) >= 1 else "owned"
house.owner = self.id
self.wealth -= house.price
self.rentPrice = 0
self.lease = None
self.houses.append(house)
for home in self.houses:
if home.id == self.lease:
home.status = "empty"
break
Agents who cannot find a decent house can look for houses to rent on the same market. The only requirement is that those houses must have been previously bought by another agent. This decision adds some restriction to the rental market in the model and thus increases the potential number of unhoused individuals. This condition might be relaxed on the next iterations of the simulation. The rental behavior of agents is defined below
def rent(self):
for house in self.market.houses:
if house.status == "rent" and house.rent <= self.budget * self.income and len(self.houses) == 0:
house.status = "rented"
self.status = "renter"
self.rentPrice = house.rent
self.lease = house.id
Then landlords request housing payments from their tenants and tenants pay their rent. The House class is much smaller and simply initialized as follows:
class House():
def __init__(self, id, price, rent):
self.id = id
self.price = price
self.rent = rent
self.owner = None
self.status = "empty"
The market is initialized with the following variables: the number of agents in the market nAgents, the number of houses nHouses, and an average level of wealth and income for the agents and an average rent and house price. The last four variables have an associated standard deviation to represent the heterogeneity of the agents and houses.
class Market():
def __init__(self, nAgents:int, nHouses:int,
income:float, wealth:float, price:float, rent:float,
incomeSD:float, wealthSD:float, priceSD:float, rentSD:float,
Time:int = 1):
self.nAgents = nAgents
self.nHouses = nHouses
self.income = income
self.wealth = wealth
self.price = price
self.rent = rent
self.incomeSD = incomeSD
self.wealthSD = wealthSD
self.priceSD = priceSD
self.rentSD = rentSD
self.houses = []
self.agents = []
self.time = 0
self.Time = Time
self.seed = 2025
self.min = 0.2
self.max = 0.6
self.data = Data(self, nAgents, Time)
The income and wealth levels of each agent are normally distributed, and the budget constraint is uniformly distributed on the interval between $0.2$ and $0.6$. The rent and house prices are also normally distributed with the standard deviation defined in the initialization of the class.
def create(self):
np.random.seed(self.seed)
for i in range(self.nAgents):
income = np.random.normal(self.income, self.incomeSD)
wealth = np.random.normal(self.wealth, self.wealthSD)
budget = abs(np.random.uniform(self.min, self.max))
agent = Agent(i, self, income, wealth, budget)
self.agents.append(agent)
for i in range(self.nHouses):
price = np.random.normal(self.price, self.priceSD)
rent = np.random.normal(self.rent, self.rentSD)
house = House(i, price, rent)
self.houses.append(house)
Results
The most interesting result in this simulation is to look at the evolution the statuses of agents over time. The figure shows that most agents who change status become owner from the first step of the simulation while very few rent. The most surprising result is the number of unhoused individuals that drops in the first period but remains fairly consistent later on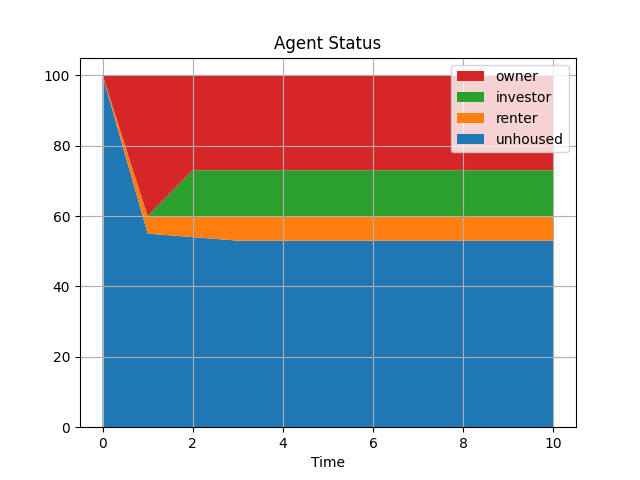
Figure $1$: Evolution of the status of agents over time. The seed is $2025$.. The simulation contains $100$ agents and $100$ houses. The agents were endowned with an average income of $20000$ and an average wealth of $1000000$. The average house price was $1000000$ and the average rent was $10000$.
This is the first iteration of the project but over time, I will improve the behavior of the agents. From the second period onwards, the results of the simulation do not change which could also be the consequence of problems in the data collection. The results remain quite similar if I change the seed.